The Moon's Rotation

Preface:

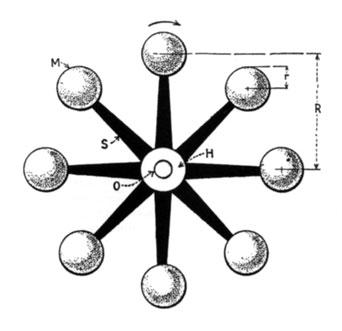
We believe the accompanying illustration and its explanation will dispel all doubts as to whether the moon rotates on its axis or not. Each of the balls, as M, depicts a different position of, and rotates exactly like, the moon keeping always the same face turned towards the center O, representing the earth.

But as you study this diagram, can you conceive that any of the balls turn on their axis? Plainly this is rendered physically impossible by the spokes. But if you are still unconvinced, Mr. Tesla’s experimental proof will surely satisfy you. A body rotating on its axis must contain rotational energy. Now it is a fact, as Mr. Tesla shows, that no such energy is imparted to the ball as, for instance, to a projectile discharged from a gun. It is therefore evident that the moon, in which the gravitational attraction is substituted for a spoke, cannot rotate on its axis or, in other words, contain rotational energy. If the earth’s attraction would suddenly cease and cause it to fly off in a tangent, the moon would have no other energy except that of translatory movement, and it would not spin like the ball. — Editor.

Article:

Since the appearance of my article entitled the “Famous Scientific Illusions” in your February issue, I have received a number of letters criticizing the views I exprest regarding the moon’s “axial rotation.” These have been partly answered by my statement to the New York Tribune of February 23, which allow me to quote:

In your issue of February 2, Mr. Charles E. Manierre, commenting upon my article in the Electrical Experimenter for February which appeared in the Tribune of January 26, suggests that I give a definition of axial rotation.

I intended to be explicit on this point as may be judged from the following quotation: “The unfailing test of the spinning of a mass is, however, the existence of energy of motion. The moon is not posest of such vis viva.” By this I meant that “axial rotation” is not simply “rotation upon an axis nonchalantly defined in dictionaries, but is a circular motion in the true physical sense — that is, one in which half the product of the mass with the square of velocity is a definite and positive quantity. The moon is a nearly spherical body, of a radius of about 1,087.5 miles, from which I calculate its volume to be approximately 5,300,216,300 cubic miles. Since its mean density is 3.27, one cubic foot of material composing it weighs close on 205 lbs. Accordingly, the total weight of the satellite is about 79,969,000,000,000,000,000, and its mass 2,483,500,000,000,000,000 terrestrial short tons. Assuming that the moon does physically rotate upon its axis, it performs one revolution in 27 days, 7 hours, 43 minutes and 11 seconds, or 2,360,591 seconds. If, in conformity with mathematical principles, we imagine the entire mass concentrated at a distance from the center equal to two-fifths of the radius, then the calculated rotational velocity is 3.04 feet per second, at which the globe would contain 11,474,000,000,000,000,000 short foot tons of energy sufficient to run 1,000,000,000 horsepower for a period of 1,323 years. Now, I say, that there is not enough of that energy in the moon to run a delicate watch.

In astronomical treatisies usually the argument is advanced that “if the lunar globe did not turn upon its axis it would expose all parts to terrestrial view. As only a little over one-half is visible it must rotate.” But this inference is erroneous, for it only admits of one alternative. There are an infinite number of axis besides its own in each of which the moon might turn and still exhibit the same peculiarity.

I have stated in my article that the moon rotates about an axis passing thru the center of the earth, which is not strictly true, but it does not vitiate the conclusions I have drawn. It is well known, of course, that the two bodies revolve around a common center of gravity, which is at a distance of a little over 2,899 miles from the earth’s center.

Another mistake in books on astronomy is made in considering this motion equivalent to that of a weight whirled on a string or in a sling. In the first place there is an essential difference between these two devices tho involving the same mechanical principle. If a metal ball, attached to a string, is whirled around and the latter breaks, an axial rotation of the missile results which is definitely related in magnitude and direction to the motion preceding. By way of illustration — if the ball is whirled on the string clockwise ten times per second, then when it flies off, it will rotate on its axis ten times per second, likewise in the direction of a clock. Quite different are the conditions when the ball is thrown from a sling. In this case a much more rapid rotation is imparted to it in the opposite sense. There is no true analogy to these in the motion of the moon. If the gravitational string, as it were, would snap, the satellite would go off in a tangent without the slightest swerving or rotation, for there is no moment about the axis and, consequently, no tendency whatever to spinning motion.

Mr. Manierre is mistaken in his surmise as to what would happen if the earth were suddenly eliminated. Let us suppose that this would occur at the instant when the moon is in opposition. Then it would continue on its eliptical path around the sun, presenting to it steadily the face which was always exposed to the earth. If, on the other hand, the latter would disappear at the moment of conjunction, the moon would gradually swing around thru 180° and, after a number of oscillations, revolve, again with the same face to the sun. In either case there would be no periodic changes but eternal day and night, respectively, on the sides turned towards, and away from, the luminary.

Some of the arguments advanced by the correspondents are ingenious and not a few comical. None, however, are valid.

One of the writers imagines the earth in the center of a circular orbital plate, having fixedly attached to its periperal portion a disk-shaped moon, in frictional or geared engagement with another disk of the same diameter and freely rotatable on a pivot projecting from an arm entirely independent of the planetary system. The arm being held continuously parallel to itself, the pivoted disk, of course, is made to turn on its axis as the orbital plate is rotated. This is a well-known drive, and the rotation of the pivoted disk is as palpable a fact as that of the orbital plate. But, the moon in this model only revolves about the center of the system without the slightest angular displacement on its own axis. The same is true of a cart-wheel to which this writer refers. So long as it advances on the earth’s surface it turns on the axle in the true physical sense; when one of its spokes is always kept in a perpendicular position the wheel still revolves about the earth’s center, but axial rotation has ceased. Those who think that it then still exists are laboring under an illusion.

An obvious fallacy is involved in the following abstract reasoning. The orbital plate is assumed to gradually shrink, so that finally the centers of the earth and the satellite coincide when the latter revolves simultaneously about its own and the earth’s axis. We may reduce the earth to a mathematical point and the distance between the two planets to the radius of the moon without affecting the system in principle, but a further diminution of the distance is manifestly absurd and of no bearing on the question under consideration.

In all the communications I have received, tho different in the manner of presentation, the successive changes of position in space are mistaken for axial rotation. So, for instance, a positive refutation of my arguments is found in the observation that the moon exposes all sides to other planets! It revolves, to be sure, but none of the evidences is a proof that it turns on its axis. Even the well-known experiment with the Foucault pendulum, altho exhibiting similar phenomena as on our globe, would merely demonstrate a motion of the satellite about some axis. The view I have advanced is NOT BASED ON A THEORY but on facts demonstrable by experiment. It is not a matter of definition as some would have it. A MASS REVOLVING ON ITS AXIS MUST BE POSEST OF MOMENTUM. If it has none, there is no axial rotation, all appearances to the contrary notwithstanding.

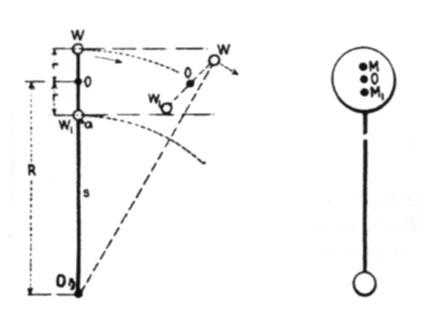
A few simple reflections based on well establisht mechanical principles will make this clear. Consider first the case of two equal weights w and w₁, in Fig. 1, whirled about the center O on a string s as shown. Assuming the latter to break at a both weights will fly off on tangents to their circles of gyration, and, being animated with different velocities, they will rotate around their common center of gravity o. If the weights are whirled n times per second then the speed of the outer and the inner one will be, respectively, V = 2 (R + r) n and V₁= 2 π (R—r) n, and the difference V—V₁ = 4 π r n, will be the length of the circular path of the outer weight. Inasmuch, however, as there will be equalization of the speeds until the mean value is attained, we shall have, V—V₁ / 2 = 2 π r n = 2 π r N, N being the number of revolutions per second of the weights around their center of gravity. Evidently then, the weights continue to rotate at the original rate and in the same direction. I know this to be a fact from actual experiments. It also follows that a ball, as that shown in the figure, will behave in a similar manner for the two half-spherical masses can be concentrated at their centers of gravity and m and m₁, respectively, which will be at a distance from o equal to 3/8 r.

This being understood, imagine a number of balls M carried by as many spokes S radiating from a hub H, as illustrated in Fig. 2, and let this system be rotated n times per second around center O on frictionless bearings. A certain amount of work will be required to bring the structure to this speed, and it will be found that it equals exactly half the product of the masses with the square of the tangential velocity. Now if it be true that the moon rotates in reality on its axis this must also hold good for EACH of the balls as it performs the same kind of movement. Therefore, in imparting to the system a given velocity, energy must have been used up in the axial rotation of the balls. Let M be the mass of one of these and R the radius of gyration, then the rotational energy will be E = ½M (2 π R n)². Since for one complete turn of the wheel every ball makes one revolution on its axis, according to the prevailing theory, the energy of axial rotation of each ball will be e = ½M (2 π r₁ n)², r₁ being the radius of gyration about the axis and equal to 0.6325 r. We can use as large balls as we like, and so make e a considerable percentage of E and yet, it is positively established by experiment that each of the rotating balls contain only the energy E, no power whatever being consumed in the supposed axial rotation, which is, consequently, wholly illusionary. Something even more interesting may, however, be stated. As I have shown before, a ball flying off will rotate at the rate of the wheel and in the same direction. But this whirling motion, unlike that of a projectile, neither adds to, nor detracts from, the energy of the translatory movement which is exactly equal to the work consumed in giving to the mass the observed velocity.

From the foregoing it will be seen that in order to make one physical revolution on its axis the moon should have twice its present angular velocity, and then it would contain a quantity of stored energy as given in my above letter to the New York Tribune, on the assumption that the radius of gyration is 2/5 that of figure. This, of course, is uncertain, as the distribution of density in the interior is unknown. But from the character of motion of the satellite it may be concluded with certitude that it is devoid of momentum about its axis. If it be bisected by a plane tangential to the orbit, the masses of the two halves are inversely as the distances of their centers of gravity from the earth’s center and, therefore, if the latter were to disappear suddenly, no axial rotation, as in the case of a weight thrown off, would ensue.